En statique, le centre de gravité est le point d'application du poids. Il s'agit d'une simplification qui consiste à considérer le poids comme une force s'appliquant en un point unique, G, plutôt que de considérer une force volumique s'appliquant en chaque point de l'objet.. Le centre de gravité est le point où toute la masse d'un objet est considérée comme concentrée. Il est important de le déterminer correctement car il influence l'équilibre, la stabilité et la maniabilité de l'objet. Voici les étapes pour calculer le centre de gravité d'un objet complexe : 1.

Séquence 7 détermination de la position du centre de gravité YouTube

CentreDeGravite.pdf Centre d'inertie Géométrie euclidienne

Calcul centre de gravité plancher moment d'inertie Autocad mémoire fin d’étude YouTube

P2 Centre de gravité orgoattiti

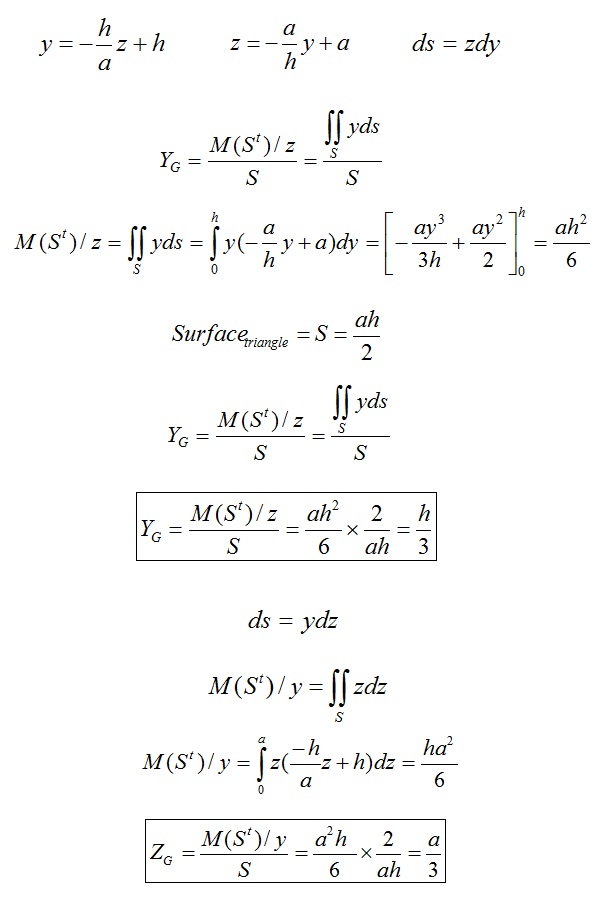
exercice calcul centre de gravité

Vidéo question Déterminer les coordonnées du centre de gravité de plusieurs masses identiques

Calcul de centre de gravité GenieCVL

Vidéo question Déterminer la position du centre de gravité d’une plaque triangulaire uniforme

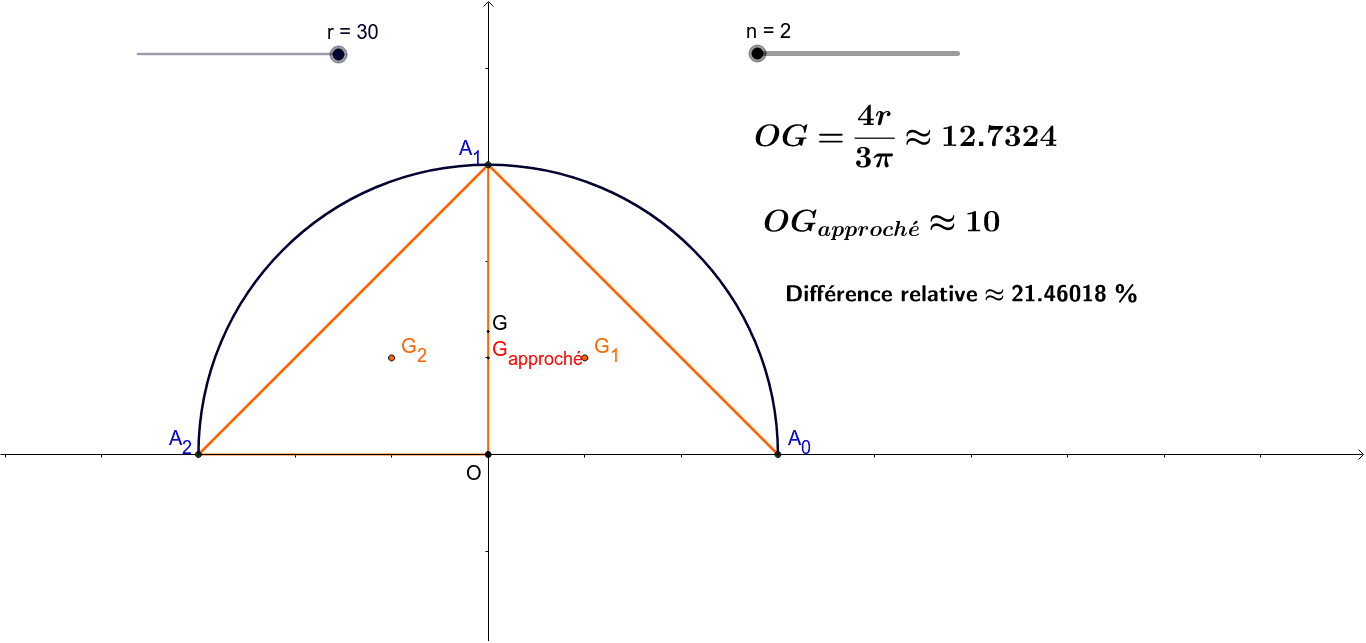
Centre de gravité d'un demidisque homogène GeoGebra

Centre de gravité

PPT Caractérisation vectorielle du centre de gravité d’un triangle PowerPoint Presentation

Centre de gravité d'un triangle rectangle AlloSchool

Vidéo question Déterminer le centre de gravité des masses ponctuelles placées sur les sommets

SST2 Partie 2 Centre de gravité YouTube

96 Déterminer la position d'un centre de gravité Demi disque YouTube

exercices corrigés centre de gravité ExoSup

NicoCivil Calcul de centre de gravité

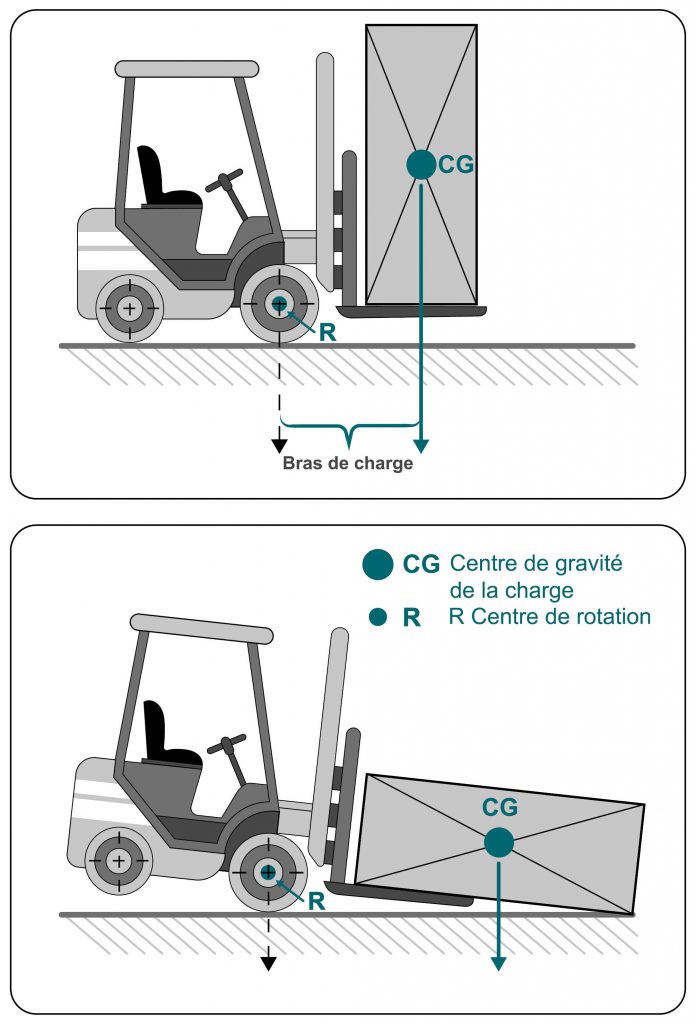
Charge chariots élévateurs

9 CALCUL DE CENTRES DE GRAVITE de POUTRES. Formules à connaître. YouTube

Centre de Gravité des solides application des systèmes de coordonnées YouTube

Pour calculer le centre de gravité global de notre système, nous devons connaître la masse relative d'une figure à l'autre. Pour ce faire, nous allons nous appuyer sur le fait que les plaques sont uniformes. Cela signifie que le rapport des aires de ces deux figures est le même que le rapport de leurs masses.. 1. Détermination d'un centre de gravité. Pour déterminer le centre de gravité de la figure 1, il faut décomposer l'élément en surfaces simples dont on connaît la position du centre de gravité : S 1, S 2, S 3, S 4. La surface de chaque rectangle ainsi définie est assimilée à une force : S 4 = 5 × 2 = 10. Construire un polygone.